本文是我在 atSwift Conf 2018 上的分享的文字版。内容和 keynote 高度重合，不过因为是文章，一些地方解释得会更加到位一些。如果看过 keynote 的同学可以不用看了。

背景

首先一个问题是：为什么要关注 Swift 在机器学习领域的应用？从语言层面来看，Swift 兼具了脚本语言快速开发迭代的特性以及 low level 的编译型语言的性能。而效率和性能是后端开发考虑的两个主要方面，所以这也不能解释为什么 Server-Side Swift 受到越来越多的关注。概括来说，Swift 具备以下优势：

高性能；
开源并且社区非常活跃，语言本身也在高速发展与迭代；
开发效率很高，并且语言级别的静态类型和异常处理使得代码非常安全；

Next Big Thing on Server

既然说到 server 开发，我们不妨认真地思考一下最近几年的 server 开发都在讨论什么，云计算和容器化极大程度的提高运维效率之外，最重要的一大改变就是基于机器学习的应用呈现出了井喷式的发展，其中主要包括以下几个方面：

推荐系统，几乎运用到了互联网的所有服务中；
文本分析，推荐系统的基础能力之一，苹果在 iOS 中也非常重视 NLP 能力的完善与建设；
音视频理解，音视频由于其数据的特殊性，长久以来我们只能从信号学层面做一些粗浅的分析，近年来得益于卷积神经网络在计算机视觉领域的成功应用，越来越多的公司在使用这些技术尝试从视频中提取更多的结构化信息；
超分辨率，简单的说就是小图变大图，曾经我们普遍使用双线性插值和双三次插值，近年来通过试用卷积神经网络技术能够更好地猜出变大后图片的细节，也有广泛的应用。
聊天机器人，这个就不用说了，智能化客服基本是已经产业化的技术，虽然有时候会被调侃为人工智障，但不可忽视的是这项技术已经切实为很多公司节省了客服的人力成本。

目前机器学习应用主要的开发语言是 C++ 和 Python，Python 用于快速验证想法，验证之后用 C++实现后部署到线上系统，这两门语言的优缺点都比较明显，C++性能很强，但门槛高，开发效率低，Python 容易写，但也非常容易写出很多垃圾代码。所谓动态类型一时爽，重构起来火葬场。

我们不禁会想，既然 Swift 是一门博众家之长的语言，那假如它能提供很好的机器学习能力，岂不是非常完美？

本文的主角解决的就是这个问题 —— Swift for TensorFlow

Swift for TensorFlow 概览

Swift for Tensor, 简称 TFiwS( 为什么这么叫，官方并没有解释，我大胆的猜测一下，应该是正读看起来像TensorFlow for Swift, 倒过来读就是 Swift)，文章接下来会简称 TFS.

TFS 是今年 Chris 在2018 TensorFlow Dev Submit 上发布的，到现在也没满一年，是一个非常年轻的技术，现在也不算正式发布，但已经开源了。目前正在 active developing 的阶段，基本上每两周会有一个新的版本放出来。

TFS 有如下几个优势：

可以融入完整的 TF 生态系统，众所周知目前 TF 的生态是最完善的；
不仅仅只是 TensorFlow 的 API binding，而是提供了 First class machine learning 的能力；
基于2中有趣的特性（后面会讲），使得 TFS 同时支持跑 CPU、GPU 以及远程的 TPU；
兼具 可用性 和 高性能；
最后一点，支持 Xcode Playground，使得天生具备“Notebook”一样的感觉；

简单的例子：

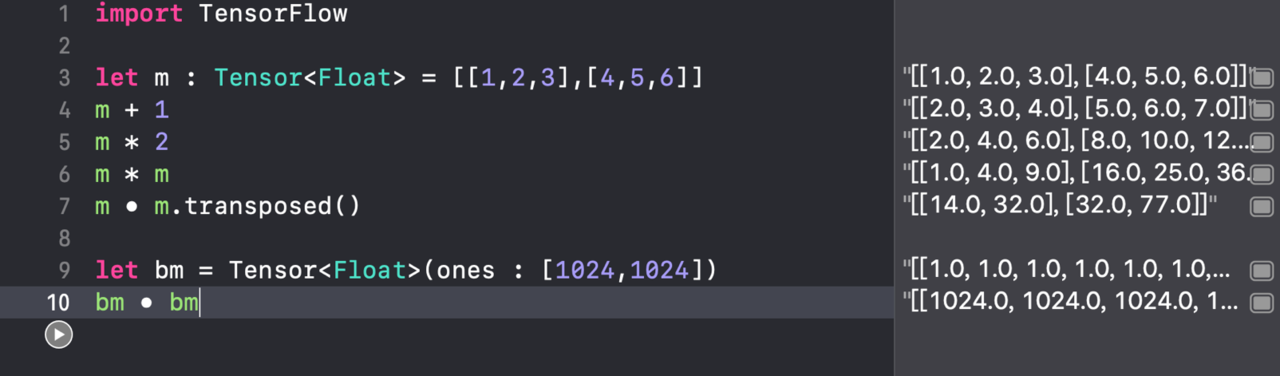
那个诡异的实心圆代表矩阵乘法，等价于 matmul

那到底什么才是所谓的“First class machine learning”, 以及为什么说 TFS 是兼具可用性和性能呢？我们还需要看 TF 的两种模式。

TensorFlow 的两种经典模式

图模式。代码如下：

#!/usr/bin/python
#coding=utf8
"""
# Author: aaron
# Created Time : 2018-09-01 16:50:36

# File Name: graph.py
# Description:

"""

import tensorflow as tf

x = tf.constant([[1,2,3], [4,5,6]])
xt = tf.transpose(x)
y = tf.matmul(x, xt)

with tf.Session() as sess:
    print sess.run(y)

图模式的一个重要特点就是：Lazy Evaluation。比如在执行 xt = tf.transpose(x) 的时候，实际上并没有触发矩阵转正的运算，而是只是生成了一个名为”转置”的运算节点，添加到了计算图中。最后，当执行 sess.run(y)的时候，所有计算才开始运行。

由于这个独特的模式，图模式的优点很明显，那就是性能很强，因为计算时已经知道了所有的计算节点，可以做很多优化，同理，缺点也明显，可用性很差，先建图后计算的模式并不符合直觉，而且只能使用节点支持的运算来构建计算图。Debug 起来很痛苦，因为你并不能通过 print x 这样的形式来 debug 一些中间变量（执行到 print 的时候 x 还没有 value）。

Eager Execution 模式。示例代码如下：

#!/usr/bin/python
#coding=utf8
"""
# Author: aaron
# Created Time : 2018-09-01 16:59:01

# File Name: eager.py
# Description:

"""

import tensorflow as tf
tf.enable_eager_execution()

x = tf.constant([[1,2,3],[4,5,6]])
y = tf.matmul(x, tf.transpose(x))
print(y)

顾名思义，Eager 模式与图相反，计算是立即发生的，整个过程并不会构建图。所以可以使用自然的流程控制，比如 if 语句来书写模型，也可以在执行的过程中插入 print x 来获取中间值，帮助我们 debug。

Eager 模式更符合直觉，易于理解，易于 debug。但因为没有 lazy，所以很难做优化，性能并不好。

第三种模式 — TFS 模式

以下是一段 Swift 代码：

    let x : Tensor<Float> = [[1,2,3], 
                             [4,5,6]]
    var y = Tensor<Float>(zeros: 
                            x.shape)
    print(y)
    if x.sum() > 100{
        y = x
    }else{
        y = x • x
    }
    print(y)

上面的代码看起来是 eager 的，但其实跑起来是以 graph 的形式跑的，所以具备图模式的所有优化。TFS 实现了一个改进版的 Swift 编译器，在编译阶段会自动分析代码中的 tensor 运算，并翻译成计算图，最终执行的时候就以图的模式运营。而且这个过程对程序员透明，也就是说：

程序员只需要当它是 eager 的模式来写代码，最终跑起来就和图模式一样快了

听起来是不是不太现实？这是什么做到的呢？我们进入下一个章节。

TFS 模式的原理：Program Slicing

上文提到，TFS 会在编译期间分析出所有的 tensor 运算，并生成计算图，我们先来看看具体是怎么做的，计算图由 TensorFlow Runtime 运行的。

简单的例子

先从一段简单的代码开始：

typealias FloatTensor = Tensor<Float>

func linear(x : FloatTensor, w : FloatTensor, b : FloatTensor) -> FloatTensor
{
    let tmp = w • x
    let tmp2 = tmp + b
    return tmp2
}

代码很直观，计算 wx + b ，只是以矩阵的形式。为了简单期间，我们没有使用变量，而是都用的常量。

如果是针对上面的代码，要怎么生成计算图的？既然 Swift 没有 runtime，我们不妨来看看其对应的 AST。

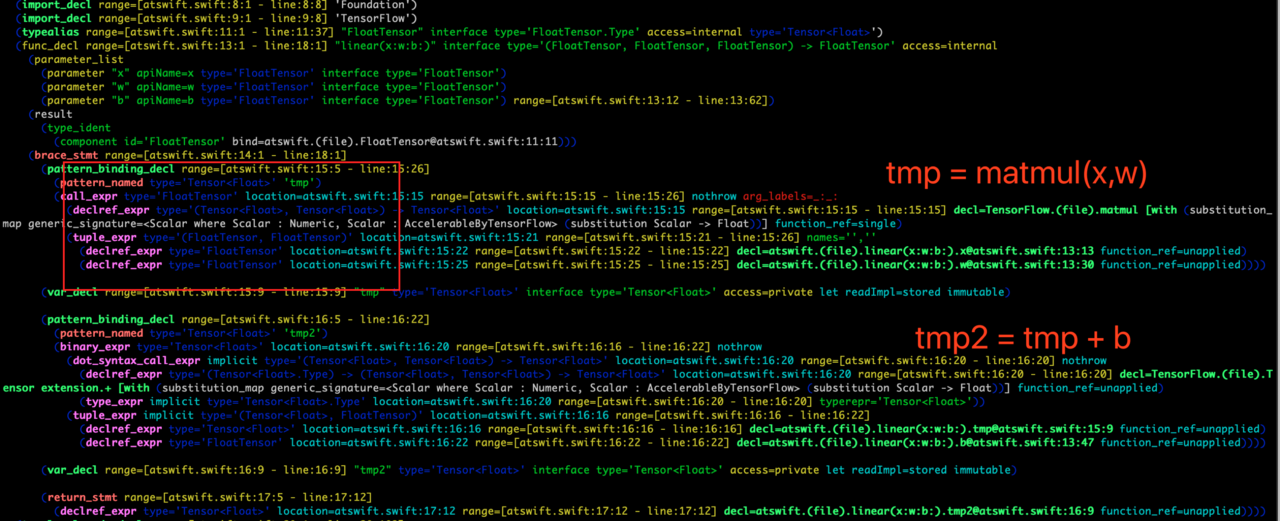
可以看到，所有 Tensor 类型的值和变量都可以从 AST 中找出来，也就是说，我们只需要遍历这个 AST，就可以得到所有 Tensor 相关的常量和对应的操作，自然就可以构建计算图。如下图所示

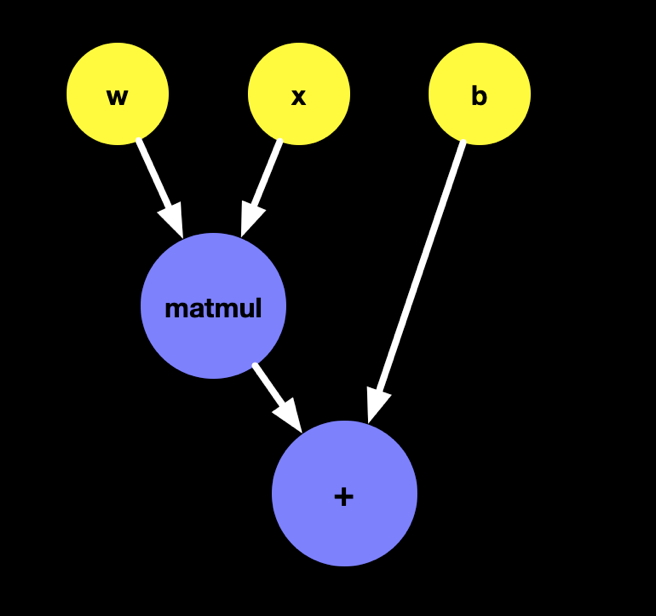
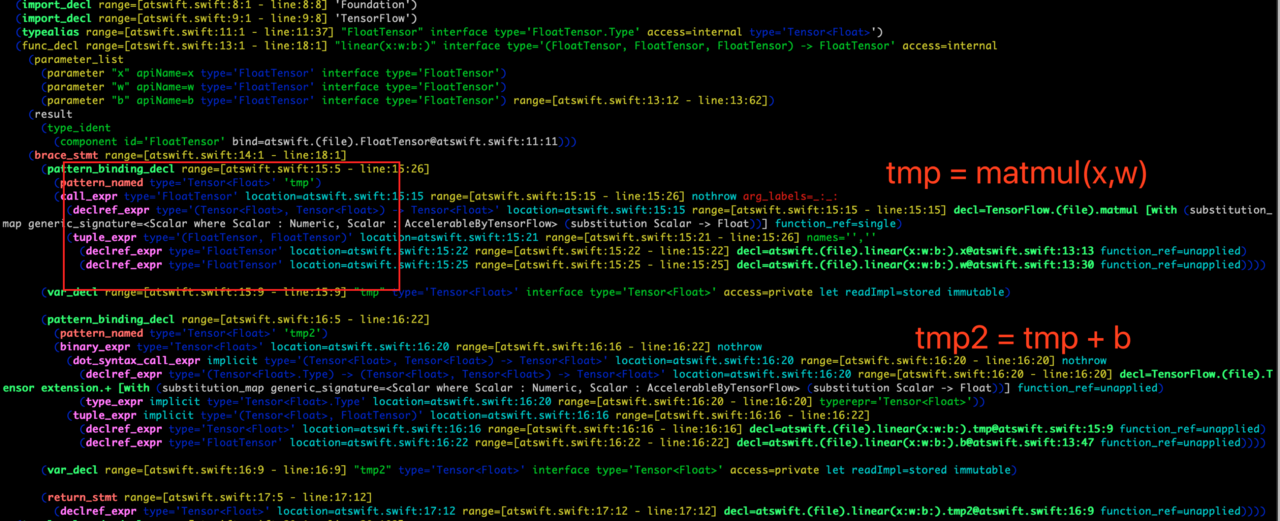
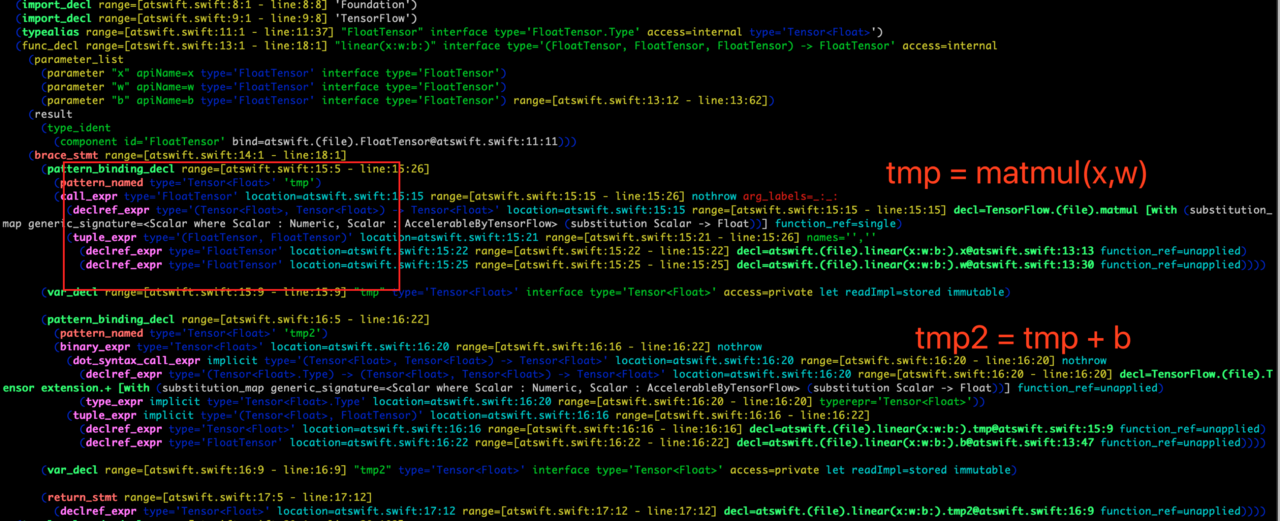以看到，这种在编译期间生成计算图的计算几乎强依赖于 Swift 的静态类型系统，所以这活儿 Python 还真不一定适合，Chris 在 TFiwS 的白皮书也介绍了为什么使用 Swift，感兴趣的可以点这里：https://github.com/tensorflow/swift/blob/master/docs/WhySwiftForTensorFlow.md

生成计算图后，代码该怎么执行呢？我们只需要将图代码移除后，替换为启动图计算的代码即可，上述代码变换后如下所示：

typealias FloatTensor = Tensor<Float>
func linear(x : FloatTensor, w : FloatTensor, b : FloatTensor) -> FloatTensor
{
    let result = execTensorFlowGraph("graph_generate_before")
    return result
}

上述代码运行时，直接调用 TensorFlow Runtime 执行刚才生成的计算图，取得执行结果后返回

复杂的例子

现在我们来看一个复杂一点的例子：

func linear(x : FloatTensor, w : FloatTensor, b : FloatTensor) -> FloatTensor
{
    let tmp = matmul(x, w)
    let tmp2 = tmp + b
    print(tmp2)
    let tmp3 = tmp2 * magicNumberGenerateFromTensor(x: tmp2)
    return tmp3
}

func magicNumberGenerateFromTensor(x : FloatTensor) -> Float
{
    return 3.0
}

和上一个例子不同的是，这里我们添加了一个真 eager 模式的代码，print(tmp2) , 不仅如此，在 tmp3的计算中，我们还耦合了 tensor 的逻辑和普通的本地运算： magicNumberGenerateFromTensor,在这样的前提下，我们生成的图是什么样的呢？

tensor逻辑，代表最终要生成 graph，由 TensorFlow Runtime 运行的逻辑，或者简单的理解为 Tensor 类的相关操作都是 tensor 逻辑。而本地运算，则是由 Swift Runtime 执行的非 tensor 逻辑的代码。

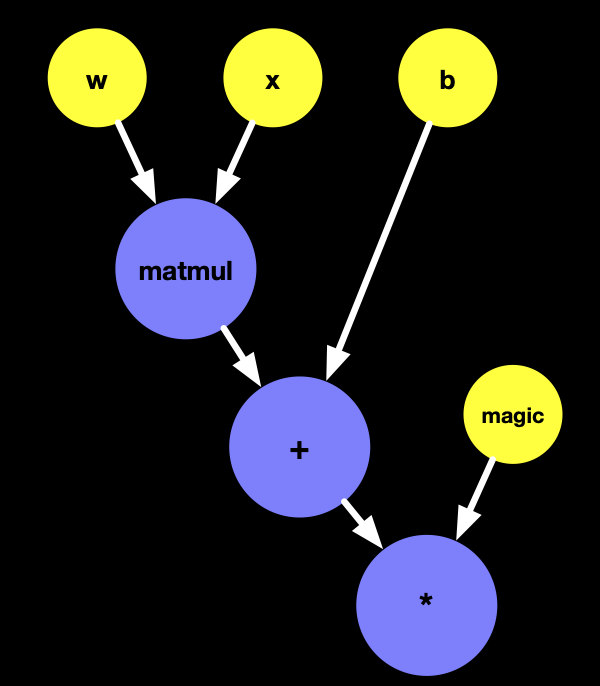
之前的思路，我们可以得到上述的图，但存在两个问题：

我们需要打印出 tmp2 ，也就是 wx+b的值，但是这个图是以一个整体由 TensorFlow 执行的，如何自动拿到某个中间的值？
magic 是由本地逻辑计算得到，TensorFlow 在执行这张图的时候，怎么知道 magic 的值到底是多少呢？

Program Slicing

接下来就是我们的 Program Slicing 技术登场了，这并不是一项新技术，但这应该是它第一次被用来干这事儿，详细介绍大家可以自行 wikipedia。

大家看完上面的问题，会发现一个终极问题是，本地代码和 graph 似乎有双向通信的需求。TFS 实现这样的双向通信，主要是通过 Program Slicing 技术，将原始代码转换为两份不同的代码，一份用来生成图，一份用来在本地跑。两份代码互相通信，完成计算。

我们再 review 一下原始代码，然后开始 slicing！

原始代码：

func linear(x : FloatTensor, w : FloatTensor, b : FloatTensor) -> FloatTensor
{
    let tmp = matmul(x, w)
    let tmp2 = tmp + b
    print(tmp2)
    let tmp3 = tmp2 * magicNumberGenerateFromTensor(x: tmp2)
    return tmp3
}

1.Graph 部分移除所有本地代码，然后针对两种情况做处理： a. 如果本地代码依赖图代码的结果，则插入 tfop(“send”, 用于指明这一步需要将结果发送给本地代码； b. 如果图代码依赖本地代码，则插入 tfop("receive"), 用于接受本地代码发过来的结果

改造完毕的图代码如下所示：

func linear(x : FloatTensor, w : FloatTensor, b : FloatTensor) -> FloatTensor
{
    let tmp = matmul(x, w)
    let tmp2 = tmp + b
    //REMOVED: print(tmp2)
    tfop("send", tmp2)
    let result = tfop("receive")
    // REMOVED: magicNumberGenerateFromTensor(x: tmp2)
    let tmp3 = tmp2 * result
    return tmp3
}

2.本地部分逻辑同上，删除图相关代码，针对依赖/被依赖的部分插入 send/receive 操作，区别只是需要在开头插入启动图代码，以及最终从图的部分拿到结果返回。

本地版本的代码

func linear(x : FloatTensor, w : FloatTensor, b : FloatTensor) -> FloatTensor
{
    let tensorProgram = startTensorGraph(graphName: "GeneratedGraphName")
    //REMOVED: let tmp = matmul(x, w)
    //REMOVED: let tmp2 = tmp + b
    let tmp2 = receivedFromTensorFlow(tensorProgram)
    print(tmp2)
    let result = magicNumberGenerateFromTensor(x: tmp2)
    sendToTensorFlow(tensorProgram, result)
    let tmp3 = finishTensorGraph(handle: tensorProgram)
    //REMOVED: let tmp3 = tmp2 * magicNumberGenerateFromTensor(x: tmp2)
    return tmp3
}

从一份代码，slice 出两份之后，将graph 部分编译成图，最终结构如下图所示：

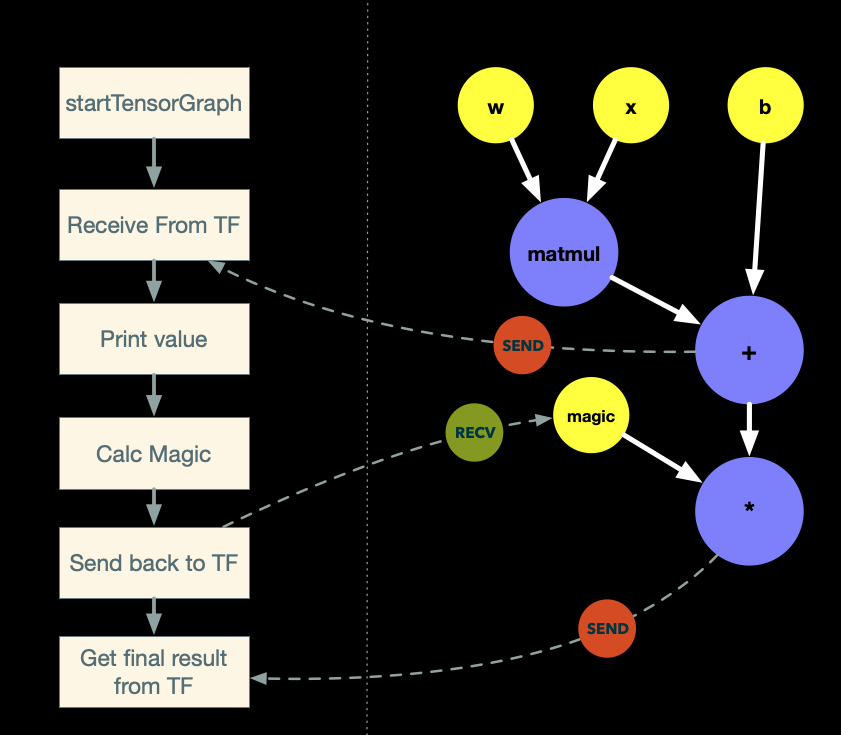
整个执行过程：

执行本地 startTensorGraph，触发图开始计算；
TensorFlow Runtime 开始计算图；
计算完毕 wx + b 后，发现有SEND 节点，于是将结果发给本地；
本地代码收到结果，如代码所写，执行 print;
本地代码调用函数，计算 magicNumber，并将结果发送给 TF Runtime；
TF Runtime 收到 magic 后，开始结算最终的结果 tmp3 ，并发回到本地；
本地收到 tmp3 ，返回结果。

以上，就实现了： 写 eager 的代码，但跑起来具备图的性能，并且像 eager 模式一样支持本地的控制流程和用 print 进行 debug。当然，背后还有很多黑魔法，这里只是讲了最简单的一个 use case……具体的大家可以去看 TFS 的白皮书。

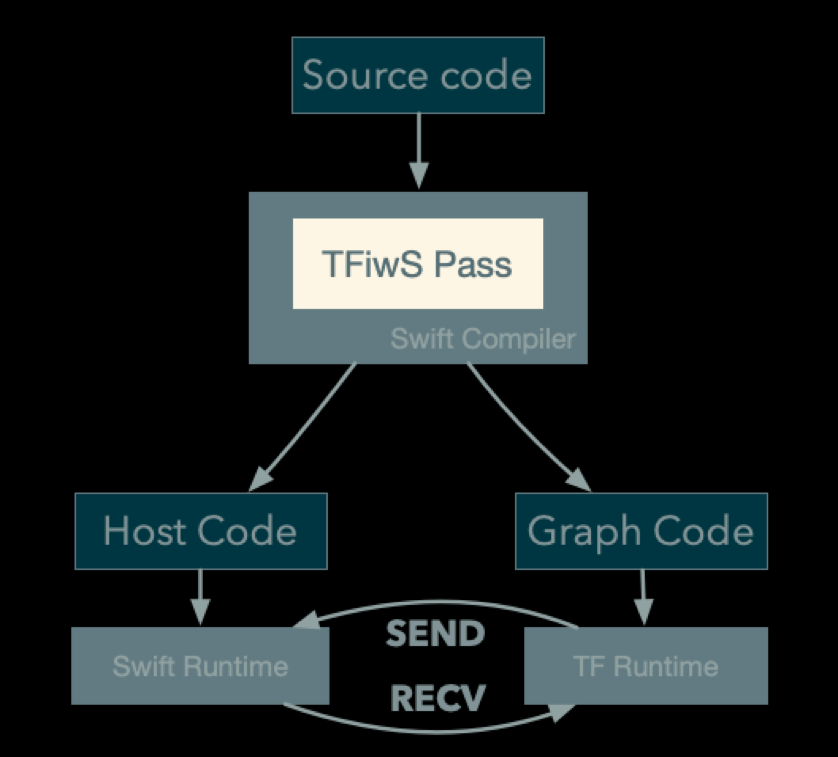
看到这里大家会想 SEND 节点和 RECV 节点是啥，为什么 TensorFlow 有这么骚的操作？其实这两个东西本来是让 TensorFlow 做分布式计算的，在不同的机器上同步结果。所以这个模式能 work，关键还是 TensorFlow 本身具备一个比较牛逼的架构。

通用的流程如下图所示：

实战 — 线性分类问题

在了解了 TFS 大致的原理之后，这里讲一个机器学习中非常基础的例子，来体验一下 TFS 开发机器学习类应用的便利性。

问题描述

海洋的某片区域受到了污染，经过了五十三次勘探，我们得到了如下的分布图：

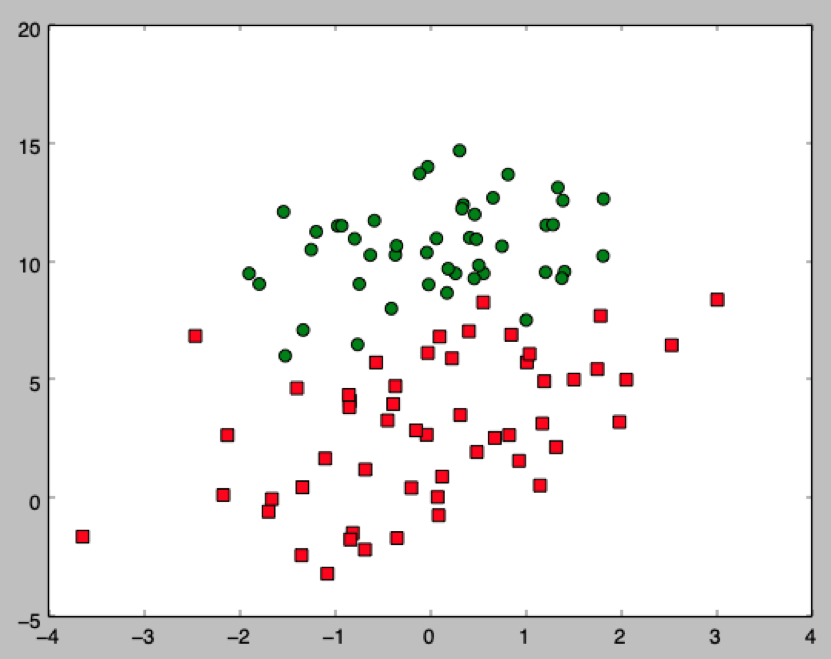
其中，绿色的圆代表该位置是干净的，红色的方块代表该位置受到了污染。

问题就是，当给一个新的坐标 (x1’, x2’) ,我们能否基于之前的勘探数据推测出该位置是否被污染？

问题分析

首先，通过观察图，很明显污染和被污染是线性可分的，那我们可以假设，我们要寻找的是一条直线，假设为 L. 我们可以得到如下的模型：

\[Line\left( X \right)=\; w_{0}\; +\; w_{1}x_{1\; }+\; w_{2}x_{2}\; =\; W^{T}X\]

之所以可以写为左右的矩阵形式，我们只需要假设存在x0并且x0恒为1，这样就可以把w0也带一个x0的系数，进而整体写成矩阵的形式。

上述模型有三个权重，w0,w1,w2，这就是我们要通过训练数据来计算的。不过现在我们先思考一个终极问题：假设我们已经有了w0~w2，我们怎么用这个线性模型来判断一个新的坐标的分类呢？

首先我们的模型 Line 的值域很明显是负无穷到正无穷，那我们要针对这样的一个连续值做分类，有两种方法：

设定一个阈值，超过阈值为0，否则为0；
使用其他函数将 Line 的值 map 到0到1之间；

很明显方法1是不合理的，因为不同的问题尺度不同，可以脑补一条夹角为45°的直线，不管你设多大的阈值，仍然可能会出现大于该阈值的点会同时包含两种分类。

机器学习一般使用方法2，通过一个叫做 sigmoid 的函数来进行映射，该函数的特征如下图所示: 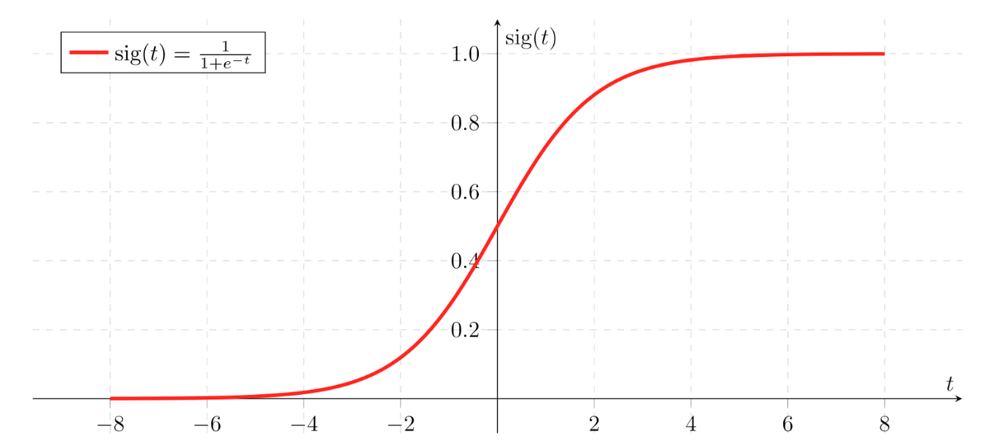从图中可以看出，这个函数的形状很完美，定义域负无穷到正无穷，值域从0到1，并且整体很平滑。我们用 sigmoid 来处理 Line 的结果，得出新的模型： \(Classifier\; =\; sigmoid\left( Line\left( X \right) \right)\; =\frac{1}{1\; +\; e^{-\left( W^{T}X \right)}\; }\;\) 既然已经知道如何用模型来计算分类了，现在是时候来计算模型本身了，如刚才所说，计算模型也就是计算 W 向量（包含三个分量）。那如何计算 W 呢？或者说什么样的 W 才是好的 W 呢？基于我们已经有了 53 次观测，于是有如下事实：

如果我们能找到一个 W，用这个 W 去计算观测点的分类，如果能尽可能的贴合我们之前实际观测到的 W，则就代表找到了一个好的 W
Classifier(X’) 的值在0-1之间，我们可以当做是 X’ 是类别1的概率

于是我们可以发现这很适合用“极大似然估计”来建模该问题，可以得到一个关于W 的方程： \(l\left( W \right)=\sum_{i=1}^{m}{\left( label^{i}\log \left( classifier\left( x^{i} \right) \right)\; +\; \left( 1\; -\; label^{i} \right)\log \left( 1\; -\; classifier\left( x^{i} \right) \right) \right)}\) 根据极大似然估计的定义，我们只需要找到一个 W，使得上述函数取得最大值，则 W 就是一个最优解。至此，我们成功的将一个分类问题，转换为一个数学上的优化问题。

找极值最常规的做法是梯度下降/上升，结合梯度上升以及对上式求导可得梯度的迭代公式： \(w_{j}=w_{j}+a\sum_{i=1}^{m}{\left( label^{i}\; -\; classifier\left( x^{i} \right) \right)}x_{j}^{\left( i \right)}\; \left( j=0..2 \right)\) 为了简化表示，通过观察上式，不难发现可以进一步写成矩阵的形式： \(W=W\; +\; aX^{T}\left( label\; -\; classifier\left( X \right) \right)\)

这个解决线性分类问题的方法也称作 logistics regression，对数几率回归。

代码实现

首先，先对我们的分类问题做一些基本的定义：

typealias FloatTensor = Tensor<Float>
let matplot = Python.import("matplotlib.pyplot")

enum Label : Int{
    case Green = 0
    case Red
}

struct ClassifierParameters : ParameterAggregate {
    var w = Tensor<Float>(randomNormal: [3,1])
}

struct Model
{
    var parameters : ClassifierParameters = ClassifierParameters()
}

这里，我们使用 TFS 中的 ParameterAggregate 结构来声明我们的模型，简单的来说就是一个 shape 为(3,1)的 tensor，代表三个 w。接下来，我们把测试数据 load 到 TFS 的 Tensor 结构中。

func loadTrainingSet() -> (trainingVec : FloatTensor , labelVec : FloatTensor)
{
    let lines = try! String(contentsOf: URL(fileURLWithPath: "test.txt")).split(separator: "\r\n")
    let data = lines.map{$0.split(separator: "\t")}
    let rowCount = data.count
    let trainingScalars:[[Float]] = data.map{[1.0, Float($0[0])!, Float($0[1])!]}
    let labelScalarts:[Float] = data.map{Float($0[2])!}
    
    let trainingVec = Tensor<Float>(shape: [Int32(rowCount), 3], scalars: trainingScalars.flatMap{$0})
    let labelVec = Tensor<Float>(shape: [Int32(rowCount) , 1], scalars: labelScalarts)
    return (trainingVec, labelVec)
}

下一步，就是最关键的训练了，我们先 review 一下我们梯度上升的核心公式： \(W=W\; +\; aX^{T}\left( label\; -\; classifier\left( X \right) \right)\)

func train(trainingVec : FloatTensor, labelVec : FloatTensor, model : inout Model){
    let learningRate:Float = 0.0005
   
    for epoch in 0...3000{
        let y = trainingVec • model.parameters.w
        let h = sigmoid(y)
        let e = labelVec - h
        let dw = trainingVec.transposed() • e
        
        let grad = ClassifierParameters(w: dw)
        model.parameters.update(withGradients: grad) { (p, g) in
            p += g * learningRate
        }

        let p1 = -1 * labelVec * log(h)
        let p2 = (1 - labelVec)*log(1 - h)
        let traditionalLogLoss = ((p1 - p2).sum() / batchSize)

        print("epoch: \(epoch), LogLoss v2: \(traditionalLogLoss)")
    }
}

大家可以很容易看到，for 开头的四个 let，其实就是用非常简单的方式实现了核心的迭代公司。虽然我们分析得很复杂，但最终整个过程实现却非常简单，必须感谢矩阵这种东西，避免了无数的 for 循环。

最后，在得到 w 之后，我们可以把我们通过模型找到的直线画出来

func plot(trainVec : FloatTensor, labelVec : FloatTensor, parameters : ClassifierParameters)
{
    //Calculate points based parameters (w0, w1, w2)     //…

    let matplot = Python.import("matplotlib.pyplot")

    let fig = matplot.figure()
    let ax = fig.add_subplot(111)
    ax.scatter(coord1x, coord1y, 50, "red", "s")
    ax.scatter(coord2x,coord2y,50, "green")
    ax.plot(xpts, ypts)
    matplot.show()
}

最终的效果如图所示：

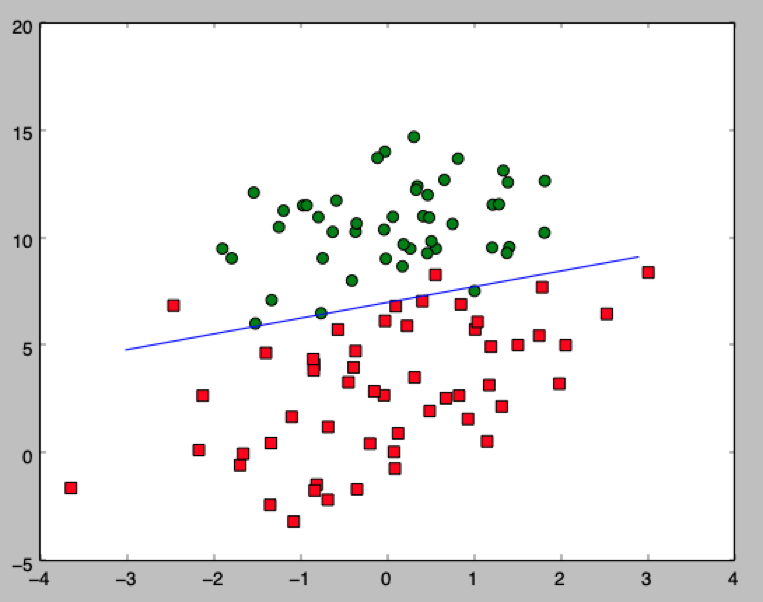
线性分类的完整代码在这里：https://github.com/aaaron7/tfiws_snippet 有兴趣的童鞋可以下来跑一跑。

总结

Swift for TensorFlow 通过一系列有趣的技术，给 Swift 带来了内置的机器学习能力，实现了高可用性以及高性能，即便现在非常早期，支持的 TF Api 还不够全，但已经能够做出很多非常有趣的事情了。

TFS 的原理，更是 Programming language 和 machine learning 一次有趣的碰撞，有兴趣可以去看看白皮书，是很有想象空间的一个方向。

Athrun & Aaron

the done is done

Swift for Tensorflow

背景