背景

KMP 是经典的字符串匹配算法，数据结构的课上会讲，但绝大多数讲述的方式都很违反直觉并直接导致很容易忘记。除了课本，很多博客也都会分析原理和执行过程，不过并没有改善，绝大多数讲的也基本和课本差不多，很多上来就给一个公式+部分匹配表，反正我是看不懂。基于此，在这里，分享一下我的分析过程。

首先要明确的一点是，KMP 算法本身包含两个步骤：

KMP 算法本身的思想与策略；
利用动态规划的思想来求一个字符串所有前缀子串的最大共同前后缀子串的长度（也就是一直在说的 next 数组）；

两个部分其实关系不大，但很多文章都很喜欢将其混在一起讲。我们首先先讲第一步。

朴素的字符串匹配

以 leetcode 28 为例，实现 substr, 在字符串 haystack 中，找字符串 needle 的位置，不存在则返回-1.

最符合直觉的方法就是穷举法，遍历 haystack 中每个字符，对于每个字符，都尝试以该字符作为开始于 needle 进行逐个字符串的比较，匹配上了则返回当前的 i。整个过程可以看做是模式串（needle）从对齐 haystack 第一个字符开始逐步一个一个往后移动的过程。

假设 haystakc=”Hello Hella”, need=”Hella”, 过程如下:

i=0:
Hello Hella
Hella

i=1:
Hello Hella
 Hella

i=6:
Hello Hella
      Hella(matched)

整个过程一共执行了 6 次检查。朴素的匹配方式实现版本如下：

 	int strStr(string haystack, string needle) {
		if (needle.empty()){
			return 0;
		}
		
		if (needle.length() > haystack.length()){
			return -1;
		}

		int i = 0;
		
		while(i<haystack.length()){
			if (haystack.length() - i < needle.length()){
				return -1;
			}
			int j = 0;
			for (j =0 ;j<needle.length();j++){
				if (haystack[i+j] != needle[j])
					break;
			}
			
			if (j >= needle.length()){
				return i;
			}
			i += 1;
		}
		return -1;
	}

尝试优化

分析一下刚才 i=0 的执行过程。H、e、l、l 都匹配成功，仅最后的 o 和 a 匹配失败。此时移动模式串 Hella，我们很容易发现接下来的几步（i=1到 i=5）都是徒劳无功，我们是否可以利用先验知识（比如 Hell 之前已经匹配成功）来避免这几次比较的浪费呢？

首先做一个大胆的假设，当基于主串的第 i 个字符，一旦模式串的第 j 位匹配失败。当 j>0时，则主串的 [i, i+j)区间直接跳过，从 i+j位置开始搜索，当 j 小于=0 时，则直接从 i+1的位置开始搜索，简单的来说就是比如有：

i=0
Hello Hella
Hella(此时 j = 4, 代表模式串第五位匹配失败)

则下一次直接从 i+j = 4位置开始搜索

i=4
Hello Hella
    Hella(j=0，失配，下一次 i=i+1 = 5)

i=5
Hello Hella
     Hella(j=0，失配，下一次 i=i+1 = 6)

i=6
Hello Hella
      Hella(matched)

基于我们的假设，整个循环次数从 6 次减少为 4 次。这个假设的核心思想就是，某次失败的匹配中已经部分匹配的内容，认为这些内容不会出现在最后的匹配中，直接丢弃（跳过）

BAD CASE

上面的是一个假设，有没有可能存在不满足该假设的 bad case 呢。比如看以下的例子, 主串=”HelloHelloHead” 模式串=”HelloHead”

i=0
HelloHelloHead
HelloHea (a 和 l 不匹配，此时 j=7)

按照刚才的公式，直接跳过已经匹配好的部分，跳到 i+j = 7处开始下一次匹配

i=7
HelloHelloHead
       HelloHead (匹配失败，i=i+1)

i=8
HelloHelloHead
        HelloHead (匹配失败)

我们知道这个 case 应该是能够匹配成功才对，但是按照我们的假设流程却失败了。通过分析过程能够发现，本质上是我们跳过得太多了。那到底要跳过多少比较合适呢？先回头看看例子

i=0
HelloHelloHead
HelloHea (a 和 l 不匹配，此时 j=7)

j=7 的位置不匹配，但能看到前面两个位置是 H 和 e并且是匹配成功的，加上模式串的开头，也是 H 和 e，看起来可以**直接把开头的 He，对齐到后面的 He**，也就是i=5 的位置

i=5
HelloHelloHead
     HelloHead(matched)

那更新一下我们的假设，当匹配失败时，直接跳到 i+j的位置开始新的匹配，但对于某些case，需要少跳几步

KMP 算法

KMP 算法的本质就是定义了什么样的情况需要少跳，以及具体少跳几步。

其实从刚才的 case 不难发现，需要少跳的步数就是模式串已经成功匹配的部分的共同前后缀的长度，比如刚才的 HelloHead，已经成功匹配的部分是 HelloHe，这个字符串具备共同的前后缀 He，长度为2.

共同的前后缀简单的理解就是前缀和后缀相同的字符串，比如 ABBA，共同前后缀是 A； ABBABB，共同前后缀是 ABB；ABBABBAAC, 无共同前后缀。

基于此，我们进一步更新我们的假设，当匹配失败时，如果已经匹配的模式子串无共同前后缀，则直接跳到 i+j的位置开始新的匹配，若存在共同子串，则跳转到 i+j-共同子串长度的位置开始新的匹配

因为模式串每一位都可能发生失配，所以我们需要求出模式串所有前缀子串分别的最大相同前后缀子串长度。比如模式串是 ABCDABC，我们需要分别求出 A、AB、ABC、ABCD、ABCDA、ABCDAB、ABCDABC 分别的最大相同前后缀的长度，比如 ABCDAB 是 2（AB），ABCDABC是 3（ABC），而 ABCDA 是 1(A)。这部分最后的结果存放在一个数组，普遍称之为 next 数组（千万别去纠结为什么叫 next）。

求最大相同前后缀的方法，朴素的可以分别生成前缀子串和后缀子串进行匹配可以得出，但这样效率比较慢，而且存在重复匹配。

KMP 算法 —— 动态规划的思想求 next 数组

既然利用动态规划思想，我们首先需要寻找最优子结构，即如何把一个问题拆解为子问题。那这个例子来说，我们需要思考当我们知道 next[i]的情况下如何求解 next[i+1]。

求解过程如下：

首先我们设一个临时变量 j，让其等于 next[i], 也就是 j=next[i] = [0,i-1]这个前缀子串的最大相同前后缀子串长度。假设模式串为 s，即 s[0,j-1] == s[i-j,i-1]；
这个时候我们要求 next[i+1], 即把 s[i] 这个字符加到 s[0,i-1] 这个子串末尾后，最大相同前后缀的子串长度。这个时候就有两个分支；
如果有 s[i]==s[j],基于 1 点末尾的等式, 则有 s[0,j]== s[i-j,i]。那显然新的子串的最大相同前后缀子串长度就是上一次迭代的结果+1，即 next[i+1] = next[i]+1;
如果 s[i]!=s[j]，则代表位置 i 之前已经匹配的、长度为 j 的最大子串已经 gg 了，所以需要去寻找新的最大相同前后缀子串长度，这里设该新的长度为k，显而易见k 肯定小于 j，因为 s[i]和 s[j]已经失配了，所以 k 只可能出现在[0,j)这个空间
那这个 k 怎么找呢？其实我们只需要做一个简单的转换，就会发现 k 其实就是 next[j], 具体如图：

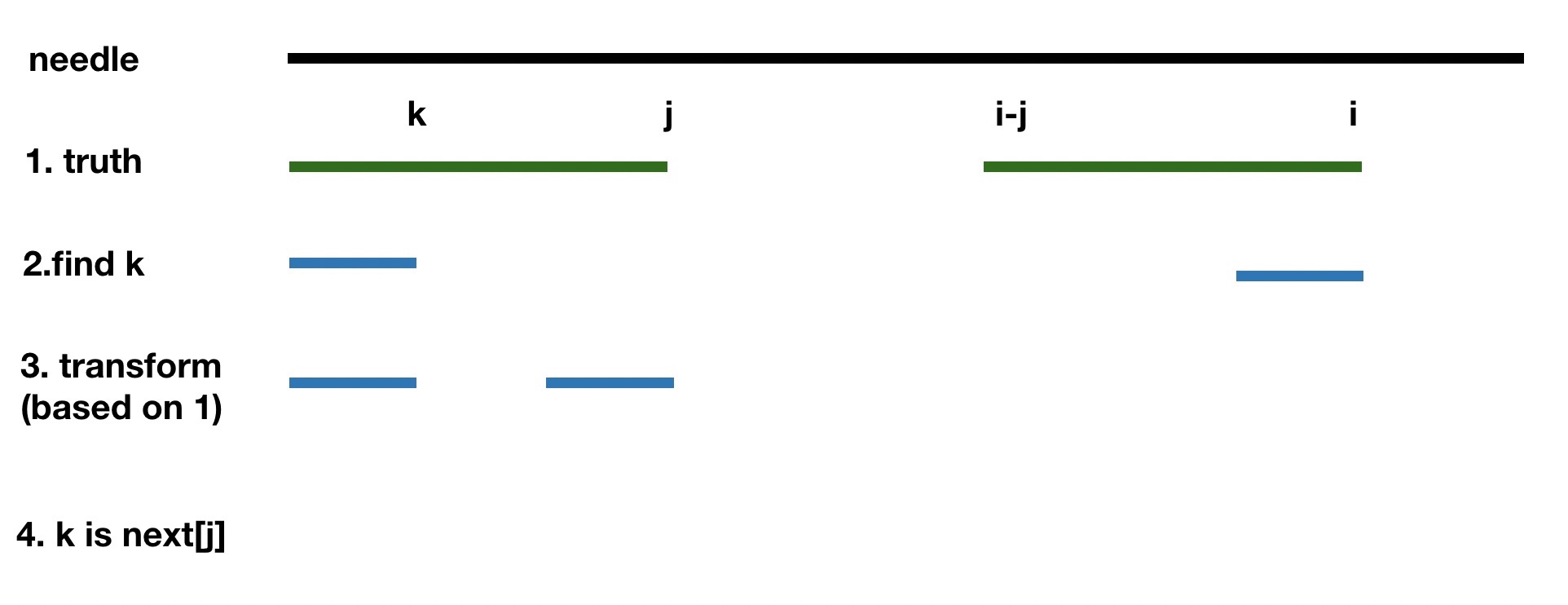
核心就是根据两条绿色区域相等，所以可以将对 k 的求值转换为在第一条绿色线条空间内进行，之后根据我们对next 的定义，即可轻松得出 k = next[j]

刚才的过程举个例子:

我们有模式串：
abcabdssabcabceqqq
            ↑

假设执行到 a 的位置，此时 i= 12， next[i] = j = 4, [0,i-1]的最大相同前后缀子串为 abca。

现在来求 next[i+1], 也就是 next[13], 比较 s[i] 和 s[j], 都是 b,相等，则 s[13] = s[12] + 1 = 5 ，最大相同前后缀子串为 abcab

abcabdssabcabceqqq
             ↑
下一步，i 更新为13,j更新为 5，s[i]为 c，而 s[j]是d，不相等，则开始寻找 k，按照刚才的流程，首先更新 k 为 next[j]，也就是 next[5]，明显这里 next[5] = 2，最大相同前后缀子串为 ab。 于是我们更新 j 到 k 的值，也就是 2.

更新完 j 后继续测试 s[i] 与 s[j], 都等于 c。于是更新 s[i+1] = s[j]+1 = 3, 也就是 s[14]的 next 值为 3， 最大相同前后缀子串为 abc.(这一步)， 如果不相同则继续下探 j 的值（j=next[j]）

到现在，我们已经实现了如何基于 next[i] 求得 next[i+1], 接下来只需要分析初始值，比如当 i=0时，此时没有子串，故 j为-1.之后每次搜索当一直失配，j 都会因为不断=next[j]，进而进入初始化逻辑，赋值为 0.

最终完整的 kmp 代码如下：

	vector<int> getNext(string needle){
		vector<int> result(needle.length());
		
		int i = 0,j=-1;
		result[0] = -1;
		while(i < needle.length() - 1){
			if (j == -1 || needle[i] == needle[j]){
				i++;
				j++;
				result[i] = j;
			}else{
				j = result[j];
			}
		}
		
		return result;
	}
	
	int strStr(string haystack, string needle) {
		if (needle.empty()){
			return 0;
		}
		
		if (needle.length() > haystack.length()){
			return -1;
		}
		vector<int> next = getNext(needle);
		
		int i = 0;
		
		while(i<haystack.length()){
			if (haystack.length() - i < needle.length()){
				return -1;
			}
			int j = 0;
			for (j =0 ;j<needle.length();j++){
				if (haystack[i+j] != needle[j])
					break;
			}
			
			if (j >= needle.length()){
				return i;
			}
			i += j - next[j];
			
			//检查已经匹配的部分是否存在共同前后缀
			
		}
		return -1;
	}

最后，祝大家中秋快乐。

Athrun & Aaron

the done is done

可能是最容易理解的 KMP 教程

背景

朴素的字符串匹配

尝试优化

BAD CASE

KMP 算法

KMP 算法 —— 动态规划的思想求 next 数组